現代的アート人物辞典:やっぱり分からない「エッシャー」

不思議な理解不能ですが技術的になんかすごいと思わされるエッシャーの作品について紹介しています。

エッシャーと言えばこの作品が有名。しかし私達はエッシャー作品によく分からない。
マウリッツ・コルネリス・エッシャー(Maurits Cornelis Escher, 1898年6月17日 - 1972年3月27日)はウッドカット、リトグラフ、メゾティントなどの版画製作でよく知られたオランダの画家(版画家)である。建築不可能な構造物や、無限を有限のなかに閉じ込めたもの、平面を次々と変化するパターンで埋め尽くしたもの、など非常に独創的な作品を作り上げた。
出典: ja.wikipedia.org
様々な技法を使って作品を制作していた模様。

また作者の顔もよく知っていなかった。
その深い洞察力と探究心から生み出された対称構造や階層構造、連続、無限や0といった概念の表現は物理学者、数学者などの間に多くのファンを持つ。
出典: d.hatena.ne.jp
絵画系じゃない方にも支持されているとはある種のカリスマです
「数学的画像」とよばれるエッシャー独特の世界
出典: kotobank.jp
数学的画像?
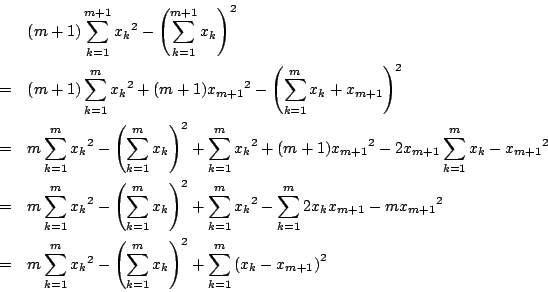
こんな複雑な事をエッシャー絵の中でやっていたのでしょうか? だから数学学者にも支持されてるのかもしれませんが。
シンメトリーや群論との結びつきを意識して勉強したいのですが、なかなか
「エッシャー」の側から調べていても道筋はありません。
出典: www.amazon.co.jp
エッシャーの魅力を数学的観点から見るのは何も珍しいことではないようです。

シンメトリー…それは一部の人から見たら気持ちが悪くなるようなものかもしれません。
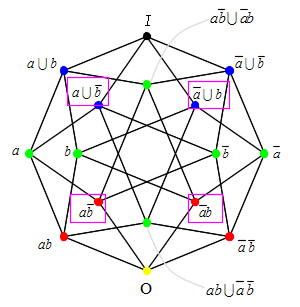
これが「群論」だそうです。
気持ちが悪くなる事はありませんが、ナンノコッチャと頭が混乱しそうです。
つまり群論とは
群論(ぐんろん、英語: group theory)とは、群を研究する学問。 群の概念は抽象代数学における中心的な概念。
出典: ja.wikipedia.org
つまりエッシャーの作品は何らかの群れが一定のシンメトリーなど法則性で集まっているようです。
それを踏まえてエッシャーの作品画像

実際には不可能だからそれをどう数学的に群論で解くのでしょうか?

幻想的でありますが、この世界が羨ましいとは思えません。
数学学者でない限り、私達がエッシャーの作品をそれで読み解こうとしたら作品に対してますます混乱する事が分かりました。

